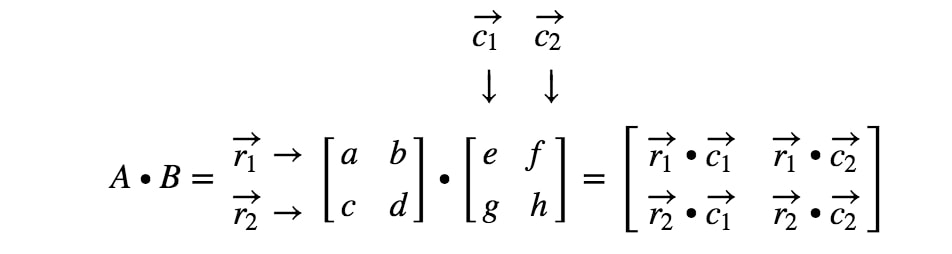The matrices involved in such multiplication are called multiplicative inverses of each other.
To multiply matrices they need to be in a certain order. In this lesson, we are only going to deal with 2×2 square matrices.i have prepared five (5) worked examples to illustrate the procedure on how to solve or find the inverse matrix using the formula method. Numpy processes an array a little faster in comparison to the list. Next, we used the for loop to iterate those matrix values. 3x2 and 2x2 multiplication returns 3x2;

The dimension of the matrix resulting from a matrix multiplication is the first dimension of the first matrix by the last dimenson of the second matrix.
If the conditions we have been discussed are not met, matrix multiplication is not possible. Vhdl code for matrix multiplication is presented. 3x2 and 2x3 multiplication returns 3x3; Luckily, for this project, only a 2 x 2 matrix is being represented so this rule is met. This is inadequate in practice, as we allocate tons of extra memory, and multiplying a $513\times 513$ matrix takes as much time as a $1024\times 1024$ matrix. matrix 2x2 matrix multiplication calculator is an online tool programmed to perform multiplication operation between the two matrices a and b. Naïve matrix multiplication requires one multiplication for each "1" When you consider the order of the matrices involved in a multiplication you look at the digits at the extremes to "see" In this calculator, multiply matrices of the order 2x3, 1x3, 3x3, 2x2 with 3x2, 3x1, 3x3, 2x2 matrices. So if you did matrix 1 times matrix 2 then b must equal c in dimensions. Get the free 2x2 matrix determinant inverse widget for your website blog wordpress blogger or igoogle. For the rest of the page, matrix multiplication will refer to this second category. The product of a and b, denoted by ab, is the m × n matrix with its (i, j )th entry equal to the sum of the products of the corresponding elements from the ith row of a and the jth column of b.
Next multiply times the second column and add to get the second number in the first row of the answer: Your first 5 questions are on us! matrix is a square array of numbers. multiplication of one matrix by second matrix. matrix multiplication is not universally commutative for nonscalar inputs.

We will leave the explanation about inverse matrices for later lessons, starting with the topic of the inverse of a 2x2 matrix.for now, it is just important that you know this is one of the properties of identity matrix that we can use to solve matrix equations.
B %*% a ,1 ,2 1, 20 52 2, 28 76 note that the order of the matrices affects the results in matrix multiplication. Yes, it wll give you a 2xx1 matrix! In vhdl we can write each individual element as, The left column represents 2x2 matrix multiplication. To perform this, we have created three functions: matrix must equal the number of rows in the first matrix. Your text probably gave you a complex formula for the process, and that formula probably didn't make any sense to you. Of a as a matrix again. 4 × 1 + 5 × 3 = 4 + 15 = 19. You will see that ab need not equal ba even if both can be done. C (i) = sum a (x) * b (y) where x=0 to i, y=0 to j. Sometimes there is no inverse at all. That is, a*b is typically not equal to b*a.
Luckily, for this project, only a 2 x 2 matrix is being represented so this rule is met. The order of the result. 3x2 and 2x3 multiplication returns 3x3; Remember that function composition is really matrix multiplication, and that the matrix that represents the identity function is the identity matrix. matrix is a square array of numbers.

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices.
Color(red)(2)xx2 and 2xxcolor(red)(1) so the result will be a 2xx1. We performed matrix multiplication on x and y matrixes within that loop and assigned it to another matrix called multi. Remember that function composition is really matrix multiplication, and that the matrix that represents the identity function is the identity matrix. The process is messy, and that complicated formula is the best they can do for an explanation in a formal setting like a textbook. The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one. We need to use matrix multiplication (or matrix product) in the case of solving the linear system of equations, while calculating the eigenvalues and eigenvectors, while obtaining the matrix decompositions. multiplication practice packet 1x1, 2x1, 2x2, 3x1, 3x2. It is a basic linear algebra tool and has a wide range of applications in several domains like physics, engineering, and economics. matrix multiplication 3 x 2 and 2 x 2 multiplication of 3x2 and 2x2 matrices is possible and the result matrix is a 3x2. Gonna have to do some computation so this is going to be equal to this is going to be equal to i'm going to make a huge 2x2 matrix here so the way we get the top left entry the top left entry is essentially going to be it's going to be this row it's going to be this row times this product if you viewed. Yes, it wll give you a 2xx1 matrix! matrix 2x2 matrix multiplication calculator is an online tool programmed to perform multiplication operation between the two matrices a and b. Inverse of a 2×2 matrix.
Download Matrix Multiplication 2X2 Pics. matrix must equal the number of rows in the first matrix. You can multiply 2x2 identity matrices with this online calculator. 3x2 and 2x3 multiplication returns 3x3; Sometimes there is no inverse at all. They both are 3x2 matrices: