matrix chain multiplication (or matrix chain ordering problem, mcop) is an optimization problem that can be solved using dynamic programming.
It means that, if a and b are considered to be two matrices satisfying above condition, the product ab is. Similarly, the other matrix order is 4 x 3, thus the number of elements will be 12 i.e. The calculator will find the product of two matrices (if possible), with steps shown. Pointer to input matrix stored in row major order. To multiply 2 contiguous matrices of size pxq and qxm, computations required are pxqxm.

In python, we can implement a matrix as nested list (list inside a list).
To perform matrix multiplication between 2 numpy arrays, there are three methods. In this context, using strassen's matrix multiplication algorithm, the time consumption can be improved a little bit. Shows why matrix multiplication order is important. Multiplying a matrix and a vector 2:31:04 blackboard: Just to show that this property works, let's do an example. It multiplies matrices of any size up to 10x10 (2x2, 3x3, 4x4 etc.). Choose the method you like the best! In other words in matrix multiplication the order in which two matrices are multiplied matters. In order for matrix multiplication to work, the number of columns of the left matrix must equal to the number of rows of the right matrix. Printing brackets in matrix chain multiplication problem. Algorithm for location of minimum value. A = np.ones( (2, 2)) >>> But since it is associative, we always have:
Sal checks whether the commutative property applies for matrix multiplication. P 10 20 30 40 30 output. Whether the sequence as multiplied as a.(b.c) or (a.b).c ) the chain will give you the same answer, thus we say it is associative. An output of 3 x 3 matrix multiplication c program: Let the scalar k= 5 and the matrix.

Now the next property is the distributive property.
For example x = 1, 2, 4, 5, 3, 6 would represent a 3x2 matrix. Hot network questions sobolev spaces of differential forms and regular atlases is hillier f. Make sure that the the number of columns in the 1 st one equals the number of rows in the 2 nd one. While there are many matrix calculators online, the simplest one to use that i have come across is this one by math is fun. B = np.ones( (2, 2)) >>> The product is calculated by multiplying the rows of a by the columns of b element by element. After the initialization part, we are getting the order of the matrix from the user for the first matrix, then simultaneously the user has to declare the order of the second matrix. The distributive property states that: The matrix multiplication is done in the order srt, where s, r, and t are the matrices for scale, rotate, and translate, respectively. To do so, we are taking input from the user for row number, column number, first matrix elements and second matrix elements. This is assuming that the matrices are in row major. Q of order a*b and b*c are multiplied, the resultant matrix will be of the order a*c. Therefore, we have a choice in forming the product of several matrices.
matrix chain order problem matrix multiplication is associative, meaning that (ab)c = a(bc). This means that you are free to parenthesize the above multiplication however we like, but we are not free to rearrange the order of the matrices. Working of c programming matrix multiplication. In the above program, we have initialized the variables and arrays inside the main method in integer (int) data type. To multiply 2 contiguous matrices of size pxq and qxm, computations required are pxqxm.

The chain matrix multiplication problem given dimensions corresponding to matr 5 5 5 ix sequence, , 5 5 5, where has dimension,.
In this article, i break down the problem in order to formulate an algorithm to solve it. The following example is the same as the preceding example, except that append has been changed to prepend. Optimum order for matrix chain multiplications. Make sure that the the number of columns in the 1 st one equals the number of rows in the 2 nd one. Bottom up algorithm to calculate minimum number of multiplications; matrix to matrix multiplication a.k.a "messy type" To perform matrix multiplication between 2 numpy arrays, there are three methods. • given some matrices to multiply, determine the best order to multiply them so you minimize the number of single element multiplications. Consider you have 3 matrices a, b, c of sizes a x b, b x c, c xd respectively. Sal checks whether the commutative property applies for matrix multiplication. For example, 2 1 1 2 1 1 2 1 = 1 0 2 0. P 10 20 30 40 30 output. Printing brackets in matrix chain multiplication problem.
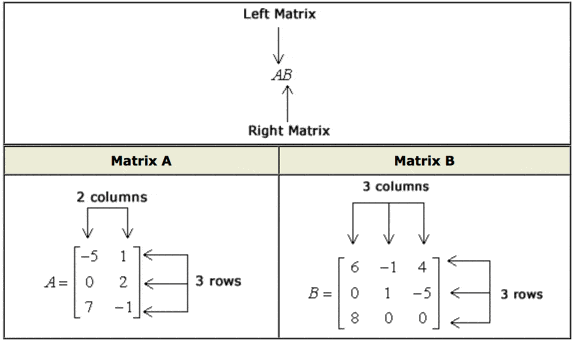
29+ Matrix Multiplication Order Background. Determine which one is the left and right matrices based on their location. Let the scalar k= 5 and the matrix. matrix multiplication is a simple binary operation that produces a single matrix from the entries of two given matrices. It means that, if a and b are considered to be two matrices satisfying above condition, the product ab is. That is, for any scalar k and the matrix amn, where m is the number of rows and n is the number of columns, then the scalar multiplication of a matrix kamn = bmn, which is given below: