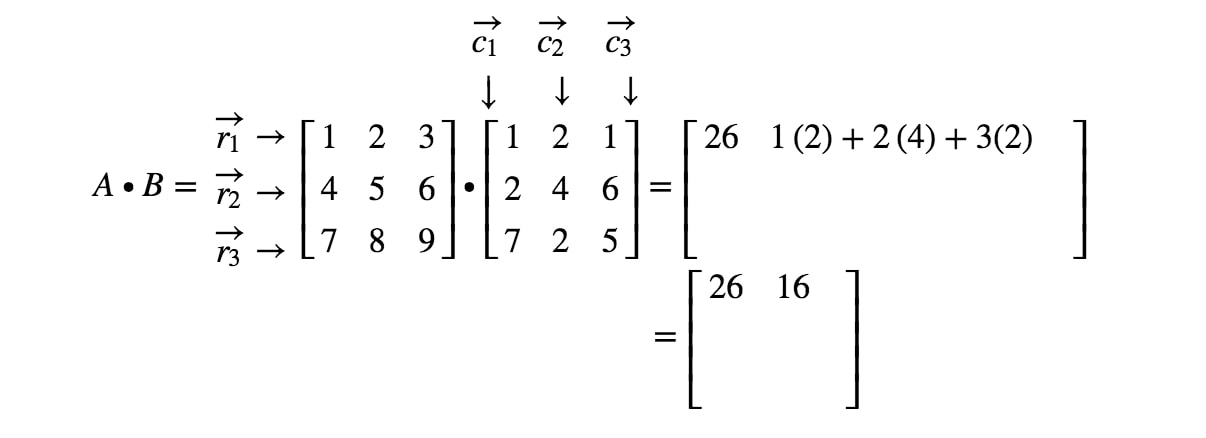View Multiplication Of Different Order Matrix Background

Matrix multiplication is associative, so you can do it in whichever order you like. · the resultant matrix will then have order . Or we can say that b is premultiplied by a. Scalar multiplication is generally easy. Demonstrates a useful technique for keeping track of matrix multiplication.

These two multiplications are completely different).

Explains how to multiply a matrix by a scalar and by another matrix. Means first multiply two matrices then another one. You can prove it by writing the matrix multiply in . These two multiplications are completely different). Multiplying a matrix by another matrix. We match the 1st members (1 and 7), multiply them, likewise for the 2nd members (2 and 9) and the 3rd members (3 and 11) . Matrix multiplication is not commutative, so the order of arguments in each multiplication matters. Or we can say that b is premultiplied by a. We work across the 1st row of the first matrix, multiplying down the 1st column of the second . The product ba is defined (that is, we can do the multiplication), but the product, when the matrices are multiplied in this order, will be 3×3, not 2×2. Matrix multiplication is not commutative, therefore ab≠ba in general (note that. · the resultant matrix will then have order . The simple form of matrix multiplication is called scalar multiplication, multiplying a scalar by a matrix.

Demonstrates a useful technique for keeping track of matrix multiplication. We work across the 1st row of the first matrix, multiplying down the 1st column of the second . The simple form of matrix multiplication is called scalar multiplication, multiplying a scalar by a matrix. Matrix multiplication is not commutative, therefore ab≠ba in general (note that. Explains how to multiply a matrix by a scalar and by another matrix.

Multiplication order · to describe the matrix product ab, we can say a is postmultiplied by b;

The product ba is defined (that is, we can do the multiplication), but the product, when the matrices are multiplied in this order, will be 3×3, not 2×2. Or we can say that b is premultiplied by a. We match the 1st members (1 and 7), multiply them, likewise for the 2nd members (2 and 9) and the 3rd members (3 and 11) . Multiplying a matrix by another matrix. Means first multiply two matrices then another one. · the resultant matrix will then have order . The simple form of matrix multiplication is called scalar multiplication, multiplying a scalar by a matrix. We multiply and add the elements as follows. Multiplication order · to describe the matrix product ab, we can say a is postmultiplied by b; If matrix a is of order m x n and matrix b is of order p x q, then matrix multiplication a x b is possible if n=p. Explains how to multiply a matrix by a scalar and by another matrix. Matrix multiplication is associative, so you can do it in whichever order you like. Matrix multiplication is not commutative, therefore ab≠ba in general (note that.

You can prove it by writing the matrix multiply in . Explains how to multiply a matrix by a scalar and by another matrix. If matrix a is of order m x n and matrix b is of order p x q, then matrix multiplication a x b is possible if n=p. Matrix multiplication is not commutative, therefore ab≠ba in general (note that. Means first multiply two matrices then another one.

Matrix multiplication is associative, so you can do it in whichever order you like.

Explains how to multiply a matrix by a scalar and by another matrix. Demonstrates a useful technique for keeping track of matrix multiplication. If matrix a is of order m x n and matrix b is of order p x q, then matrix multiplication a x b is possible if n=p. · the resultant matrix will then have order . The simple form of matrix multiplication is called scalar multiplication, multiplying a scalar by a matrix. These two multiplications are completely different). Multiplication order · to describe the matrix product ab, we can say a is postmultiplied by b; We multiply and add the elements as follows. Matrix multiplication is associative, so you can do it in whichever order you like. Multiplying a matrix by another matrix. Matrix multiplication was first introduced in 1812 by french mathematician jacques philippe marie binet, in order to represent linear maps using matrices. Matrix multiplication is not commutative, so the order of arguments in each multiplication matters. Scalar multiplication is generally easy.

View Multiplication Of Different Order Matrix Background. Matrix multiplication was first introduced in 1812 by french mathematician jacques philippe marie binet, in order to represent linear maps using matrices. We work across the 1st row of the first matrix, multiplying down the 1st column of the second . Matrix multiplication is associative, so you can do it in whichever order you like. Matrix multiplication is not commutative, so the order of arguments in each multiplication matters. If matrix a is of order m x n and matrix b is of order p x q, then matrix multiplication a x b is possible if n=p.

Demonstrates a useful technique for keeping track of matrix multiplication matrix multiplication order. Or we can say that b is premultiplied by a.